CALCULATION MODEL FOR CRITICAL VELOCITY OF SAND MOVEMENT IN DECOMPOSED HYDRATE CEMENTED SEDIMENT
-
摘要: 出砂是制约当前天然气水合物长效开发的关键因素之一。基于水合物分解区地层松散沉积物球形颗粒堆积假设，分析了水合物分解前缘和分解区内部地层砂微粒的受力情况，基于力矩平衡条件建立了松散沉积物中地层砂颗粒启动运移临界流速的计算模型，并进行模型敏感性分析。结果表明，水合物分解前缘和分解区内部微粒的临界流速均随着粒径、排布角度、颗粒摩擦系数的增加而增加，胶结物性质、流体中的电解质类型以及浓度等参数均对临界出砂流速产生一定的影响。本文建立的砂粒启动运移临界流速模型能够为水合物开采储层出砂评价提供支撑。Abstract: In the mining process of natural gas from a hydrate reservoir, sanding is one of the major factors restricting the development of natural gas hydrate. In this paper, based on the assumption that hydrate cemented sediment is composed of tightly squeezed balls in equal size, we analyzed the stress conditions of such sand particles on the leading edge and in the decomposed zone. A critical velocity model for sand migration in decomposed hydrate-cemented sediment is built then on account of torque balance conditions. The results indicate that critical velocity of particles on the leading edge and in the decomposed zone increases with the increase in particle diameter, arrangement angle and coefficient of friction, and the properties of cement and the type and concentration of electrolyte in the fluid also influence the critical velocity of sand migration. The model proposed in this paper can provide a theoretical basis for evaluation of hydrate sanding.
-
我国南海海域蕴藏大量的天然气水合物资源[1, 2]，2017年由中国地质调查局主持在我国南海神狐海域开展了首次天然气水合物试采工程，并于5月18日国土资源部宣布试采成功，这标志着我国在天然气水合物资源开发利用方面迈出了重要的一步。地层砂(泥)产出过程的精确控制是保证水合物试采成功的关键。
国内外实践均表明[3-5]，出砂问题是制约天然气水合物资源有效开发的重要因素。对于常规油气井成岩储层，通常认为出砂是指当岩石受到的剪切应力达到储层破坏条件时，固体颗粒从岩石骨架上剥落成为游离砂粒[6, 7]，并在孔隙流体压力[8]、地应力[9, 10]等综合作用下向井筒流动的过程。因此，对于常规成岩油气储层而言，目前对地层出砂临界条件的研究集中在颗粒由骨架成分剥落成为游离颗粒的临界条件方面，并认为地层在有效应力作用下发生塑性破坏的临界井底压力点和对应的储层流速分别为储层的出砂临界井底流压值和出砂临界地层流体流速值。然而，水合物储层埋深浅[11]，属于未固结或极弱固结储层，水合物完全分解后地层骨架消失，因此，水合物生产过程中地层的出砂机理完全不同于常规油气储层。天然气水合物开采过程中出砂现象的研究重点应该是在水合物分解、流体携带和上覆应力等综合作用条件下，地层固相颗粒由储层向井筒迁移的过程。
与常规油气井出砂临界条件研究相比，天然气水合物开采储层出砂临界流速计算的最大难点是：(1)目前常规岩石破坏本构不能有效地推广到天然气水合物储层[12]；(2)水合物分解区和未分解区存在本质差异，不同区域内细质颗粒启动产出的临界流速计算模式和需要考虑的影响因素都不同。但实际上，由于水合物分解过程是从井筒开始并逐渐向地层深部延伸的，实际水合物开采储层中流体渗流过程主要发生在水合物分解区内，水合物未分解区的渗流过程相对较弱。因此，以水合物分解前缘为界，可以认为水合物未分解区内的储层即使在应力条件下发生破坏，也不会造成大量的井筒出砂，而水合物分解区内的砂粒则会优先发生运移产出，是水合物开采地层出砂现象的主要响应区域。
基于上述基本假设，本文将以孔隙充填型水合物储层为基础，建立水合物分解区内松散沉积物的颗粒堆积模型，基于该模型分析水合物分解区内储层微粒的受力情况，建立松散沉积物中微粒启动运移临界流速计算模型，并进行模型敏感性分析，为水合物开采井出砂规律的分析提供参考。
1. 物理模型
根据南海水合物钻探数据，含天然气水合物松散沉积物粒径小，分选性和均匀性均较差[13, 14]，建立全尺寸粒度分布范围的水合物分解区固相颗粒启动运移模型难度较大。为了便于模型求解，可以将整个地层的松散沉积物视为等直径球形微粒堆积，如图 1a所示。天然气水合物在地层中的赋存形态大致可以分为3类[15, 16]，充填于孔隙中，作为沉积物的胶结物和作为沉积物骨架起支撑作用，本模型针对的是作为孔隙充填型水合物的情况。
![]()
图 1 天然气水合物松散沉积物中微粒示意图a.原始条件下地层微粒分布示意图；
b.水合物分解后形成的“孤立悬空”的砂粒示意图；
c.水合物分解前缘砂粒示意图；
d.水合物分解区内部砂粒示意图
蓝色微粒表示天然气水合物，黑色微粒表示地层沉积物骨架，红色微粒表示水合物分解后可能造成的游离颗粒或胶结相对较弱的砂粒Figure 1. Schematic diagram of particles in hydrate decomposed unconsolidated sediment图 1a中蓝色微粒表示天然气水合物，水合物分解之前作为固相颗粒的一部分存在，黑色微粒表示地层沉积物骨架，红色微粒表示水合物分解后可能造成的游离颗粒或胶结相对较弱的沉积物颗粒。当沉积物中的天然气水合物发生分解产出后，水合物所占据的空间将被“腾出”，形成松散沉积物中的渗流通道，松散颗粒在沉积物中有3种基本存在形态，分别如图 1b—d所示。
其中，图 1b中所示水合物分解后形成的“孤立悬空”的微粒，它与沉积物骨架微粒间没有相互的挤压，很容易随着水合物分解产生的液流启动运移离开壁面，但是在实际地层应力条件下这种情况几乎不可能存在，因此不作为水合物分解区细粒启动运移临界流速模型的重点进行讨论。
图 1c中的胶结较弱微粒处于水合物分解区与未分解区的交界处(分解区前缘)，流体流经此界面时会对处于该位置的微粒产生渗透压，当渗透压超过微粒受到的内聚力以及微粒间相互挤压产生的静摩擦力时，微粒就会在液流的“推动”作用下启动运移。d中，水合物分解区的颗粒之间发生相互挤压，嵌入到松散沉积物中，是常见的地层松散沉积物堆积类型。图 1c和图 1d分别代表水合物分解区前缘和水合物分解区内部的典型潜在启动运移颗粒，是本文的研究重点。
基于上述基本物理模型，为了简化计算，本文做如下基本假设：
(1) 水合物分解区内的沉积物为粒径相同的松散颗粒堆积而成，堆积颗粒受到地层应力的作用，以角度θ堆积；
(2) 由于气体的粘度较小，对固相砂粒的拖曳作用较小，因此本文假设固相颗粒主要是受单相水流的拖曳作用；
(3) 地层砂颗粒为标准的圆球形颗粒，不考虑地层砂颗粒圆度、棱角等参数的影响；
(4) 地层固相砂粒之间及砂粒与流体之间不发生物理化学反应。
根据上述基本物理模型，在静止状态下，可以认为图 1c和图 1d中红色标注颗粒在多种力的相互制约下处于力矩平衡状态。如果在流体渗流作用下打破上述力矩平衡条件，则微粒发生滚动从渗流通道壁面流出，造成井筒出砂。下文将分别探讨水合物分解前缘和分解区内部地层砂微粒的力矩平衡条件。
2. 数学模型
2.1 松散颗粒力矩平衡关系
如前所述，水合物分解区内地层颗粒启动运移的基本条件是所处的力矩平衡条件被打破。水合物开采过程中，分解区前缘(图 1c)与分解区内部(图 1d)准运移颗粒的基本受力情况分别如图 2a和b所示。
![]()
图 2 分解区松散沉积物中微粒受力示意图Figure 2. Force diagram of particles in unconsolidated sediment of hydrate decomposed zone图中，Fg为微粒的浮重，N；Fn表示微粒之间的相互挤压力，是上覆地层压力沿颗粒接触面法线方向的分量，N；Fh是液流渗流产生的推动力，N；Fd为水流的牵引力，N；Fe为内聚力，N；Ff是地层砂微粒之间的摩擦力，N；Fl是流体的举升力，N；
图 2a中，水合物分解前缘微粒受到液流推动力、内聚力、重力、微粒之间相互挤压压力以及微粒之间的摩擦力等5个力的作用。根据力矩平衡条件，使微粒在力的作用下绕支点B转动的临界条件即为此处的地层砂粒启动运移的临界条件，此时挤压力Fn指向支点B，力臂为0，所以对应的力矩平衡关系式为：
$$ \left( {{F}_{\text{h}}}-{{F}_{\text{e}}} \right){{r}_{\text{s}}}\sin \theta \ge {{F}_{\text{g}}}{{r}_{\text{s}}}\cos \theta +2{{r}_{\text{s}}}{{F}_{\text{r}}} $$ (1) 式中，rs为地层砂颗粒的半径，m。
图 2b中，水合物分解区内的沉积物堆积中的颗粒受到液流推动力、内聚力、重力、微粒之间相互挤压压力、液流的举升力以及微粒之间的摩擦力等6个力的作用，颗粒发生运移的临界条件是不同力矩作用下使颗粒能够绕支点C转动，同样地，微粒之间的挤压力Fn指向支点C，力臂为0，所以颗粒发生绕C点转动的力矩平衡式为：
$$ \left( {{F}_{\text{d}}}+{{F}_{1}} \right){{r}_{\text{s}}}\ge \left( {{F}_{\text{g}}}+{{F}_{\text{e}}} \right){{r}_{\text{s}}}+2{{F}_{\text{s}}}{{r}_{\text{s}}} $$ (2) 2.2 各力分量计算方法
(1) 液流牵引力
若将水合物分解区内由水合物分解产生的空隙中的流动视为Hele-Shaw流[17]，则孔隙壁面固体微粒受到的牵引力可表示为：
$$ {{F}_{\text{d}}}=\frac{\omega \pi \mu r_{\text{s}}^{2}{{{\bar{u}}}_{\text{cf}}}}{R} $$ (3) 式中，ω为流体牵引力常数，取值范围10~60；μ为流体粘度，Pa · s；ucf为平均真实渗流速度，m/s；R为水合物分解区沉积物堆积形成的孔喉半径，m。
(2) 液流举升力
由于在垂直于流速方向上液流的流速是不相等的，所以液流会对微粒产生向上的举升力作用，这个举升力并不是浮力，而是由液流的拖曳作用产生。其表达式为：
$$ {{F}_{1}}=\chi r_{\text{s}}^{3}\sqrt{\frac{\rho \mu \bar{u}_{\text{cf}}^{3}}{{{R}^{3}}}} $$ (4) 式中，χ为举升系数，根据Altmann[18]等的研究成果，松散沉积物渗流条件下取χ=1 190；ρ为流体中地层砂微粒密度，kg/m3。
(3) 微粒浮重
由于微粒处于液体环境中，所以受到液体浮力。浮重的表达式为：
$$ {{F}_{\text{g}}}=\frac{4}{3}\pi r_{\text{s}}^{3}\left( \rho -{{\rho }_{液}} \right)g $$ (5) 式中，ρ液为驱替流体的密度，kg/m3。
(4) 内聚力
微粒受到的内聚力在微观尺度上主要表现为静电力，包含微粒之间以及微粒和孔隙壁面之间的范德华力，微粒之间的双电层斥力以及色散力等，本文将主要考虑范德华力和双电层斥力的影响。根据DLVO理论[19, 20]，总电势能V等于范德华势能(分子间作用能)VLVA、双电层势能VDKR和玻恩势能VBR的总和，而静电力表达式为电势能与距离偏导数[21]，则有：
$$ {{F}_{\text{e}}}=-\frac{\partial V}{\partial s}=-\frac{\partial \left( {{V}_{\text{LVA}}}+{{V}_{DKR}}+{{V}_{BR}} \right)}{\partial s} $$ (6) $ 其中,{{V}_{\text{LVA}}}=-\frac{{{A}_{132}}}{6}\left[ \frac{2(1+Z)}{Z(2+Z)}+\ln \left( \frac{Z}{2+Z} \right) \right]$
$$ \begin{align} & {{V}_{\text{DLR}}}=\frac{\text{ }\varepsilon {{\text{ }}_{0}}D{{r}_{\text{s}}}}{4}\left[ 2{{\psi }_{01}}{{\psi }_{02}}\ln \left( \frac{1+\exp (-\kappa s)}{1-\exp (-\kappa s)} \right)- \right. \\ & \left. \left( \psi _{01}^{2}\psi _{02}^{2} \right)\ln (1-\exp (-2\kappa s)) \right] \\ & {{V}_{\text{BR}}}=\frac{{{A}_{132}}}{7560}{{\left( \frac{{{\sigma }_{LJ}}}{{{r}_{\text{s}}}} \right)}^{6}}\left[ \frac{8+Z}{{{(2+Z)}^{7}}}+\frac{+6-Z}{{{Z}^{7}}} \right] \\ & Z=\frac{s}{{{r}_{\text{s}}}} \\ \end{align} $$ 式中，A132是Hamaker常数，取值2.0×10-20 J；s为地层砂微粒之间的距离，m；ε0是真空介电常数，取值ε0=8.854×10-12 C-2 · J-1 · m-1；D是介电常数，取值水的介电常数D=78.0；σLJ是在Lennard-Jones势原子碰撞直径，σLJ=0.5 nm；κ是由溶液浓度和氯化钠的电解质价计算求得；ψ01表示微粒表面电势，取值ψ01=-30 mV；ψ02表示岩石颗粒表面电势，取值ψ02=-40 mV。
由于静电力为正表示颗粒之间的作用力为斥力，静电力为负表示颗粒之间的作用力为引力，引力的值随着微粒之间距离的增加先增加后减小的。要使液流拖曳微粒发生剥离，则需要克服微粒之间引力的最大值，所以将求出的引力的最大值作为内聚力Fe进行计算：
$$ {{F}_{e}}=-\min \left( {{F}_{e}} \right) $$ (7) (5) 液流推动力
水合物分解区前缘处的微粒受到的液流推动力来源于渗流液体对微粒的渗透压推动作用，与Hele-Shaw流产生的液流的牵引力Fd不同。液流推动力应用达西定理求解：
$$ k=\frac{1000 Q_{\mu} \Delta x}{A \Delta p} $$ (8) 式中，A为以图 1c中红色表示的微粒为中心作的单元体的截面积，m2；Δx为以图 1c中红色表示的微粒为中心作的单元体的长度，m；k为储层渗透率，m2；Δp为以图 1c中红色表示的微粒为中心作的单元体在流速方向的渗透压，Pa。
单元体受到的来自液流的推动力为F则表示为：
$$ F=A \Delta p=\frac{1000 Q_{\mu} \Delta x}{k} $$ (9) $$ N=\frac{A(1-\phi )\Delta x}{4/3\text{ }\!\!\pi\!\!\text{ }r_{\text{s}}^{3}} $$ (10) $$ k=\frac{\phi^{3}}{K S_{b}^{2}(1-\phi)^{2}} $$ (11) 式中，ϕ为水合物分解区孔隙度；K为Kozeny常数，取K=5；Sb为松散沉积物比表面，m2/m3。
等径球形颗粒岩石模型，松散沉积物比表面计算公式为：
$$ S_{b}=\frac{6}{D}=\frac{3}{r_{s}} $$ (12) 将式(12)代入式(11)得到渗透率的表达式为：
$$ k=\frac{\phi^{3}}{5\left(\frac{3}{r_{s}}\right)^{2}(1-\phi)^{2}}=\frac{\phi^{3} r_{s}^{2}}{45(1-\phi)^{2}} $$ (13) 将式(13)带入式(9)并结合式(10)得到水合物分解前缘处单个地层砂微粒所受到的液流推动力Fh为：
$$ {{F}_{\text{h}}}=\frac{F}{N}=60\ 000\text{ }\!\!\pi\!\!\text{ }\mu \frac{1-\phi }{{{\phi }^{2}}}{{r}_{\text{s}}}u $$ (14) 式中，u为水合物分解前缘处的渗流速度，m/s。
(6) 微粒间摩擦力
微粒之间会产生相互挤压，这种挤压作用表现在颗粒运动过程中即为颗粒之间的摩擦力，摩擦力的方向如图 2所示沿微粒间接触面的切线与运动趋势方向相反。上覆的压力包括海水产生的压力和微粒上覆的地层产生的压力，而上覆地层包括沉积物骨架和孔隙中的海水。产生的上覆压强作用在微粒之上，可以等效为作用于微粒接触点连线的方向的力Fn，作用面积为垂直于Fn方向的过球心的截面圆，Fn大小等于：
$$ \begin{matrix} \left. {{F}_{\text{n}}}=\left( {{\rho }_{\text{液}}} \right)gH+\varphi {{\rho }_{液}}gh+(1-\varphi )\rho gh \right)\cdot \text{ }\!\!\pi\!\!\text{ }r_{s}^{2} \\ {{F}_{\text{f}}}=m\cdot {{F}_{\text{n}}}=\left( {{\rho }_{液}}gH+\varphi {{o}_{液}}gh+(1-\varphi )\rho gh \right) \\ \cdot m\pi r_{\text{s}}^{2} \\ \end{matrix} $$ (15) 式中，m为摩擦系数；h为储层埋藏深度，m；H为海底之上的水深，m。
2.3 临界启动运移流速计算模型
(1) 水合物分解前缘处微粒启动运移临界流速计算模型
根据式(1)所示的力矩平衡条件，当水合物分解前缘处地层砂微粒达到其运移启动的临界流速的时候，其受力满足：
$$ \left( {{F}_{\text{h}}}-{{F}_{\text{e}}} \right){{r}_{\text{s}}}\sin \theta ={{F}_{\text{g}}}{{r}_{\text{s}}}\cos \theta +2{{r}_{\text{s}}}{{F}_{\text{f}}} $$ (16) 将式(5)、式(7)、式(14)和式(15)分别代入式(16)可以得到：
$$ \begin{matrix} \left( 60000\text{ }\!\!\pi\!\!\text{ }\mu \frac{1-\varphi }{{{\varphi }^{2}}}{{r}_{\text{s}}}{{u}_{{{c}_{-}}f}}-{{F}_{c}} \right)\sin \theta = \\ \frac{4}{3}\pi \Delta \rho gr_{s}^{3}\cos \theta +2{{F}_{\text{f}}} \\ \end{matrix} $$ (17) 将式(17)进行整理就可以得到水合物分解前缘处微粒运移启动临界流速uc_f为：
$$ \begin{align} & {{u}_{{{\epsilon }_{-}}f}}= \\ & \frac{{{F}_{\text{e}}}+\frac{4}{3}\text{ }\!\!\pi\!\!\text{ }\Delta \operatorname{og}r_{3}^{3}\cot \theta +\frac{2m\text{ }\!\!\pi\!\!\text{ }r_{\text{s}}^{2}\left( {{\rho }_{液}}gH+\varphi \rho 液\ gh+(1-\varphi )\rho gh \right)}{\sin \theta }}{60000\text{ }\!\!\pi\!\!\text{ }\mu \frac{1-\varphi }{{{\varphi }^{2}}}{{r}_{\text{s}}}} \\ \end{align} $$ (18) (2) 分解区内部微粒启动运移临界流速计算模型
根据式(2)所示的力矩平衡条件，当分解区内部微粒在力的作用发生运移启动时，其受力情况满足：
$$ {{F}_{\text{d}}}{{r}_{\text{s}}}+{{F}_{1}}{{r}_{\text{s}}}=\left( {{F}_{\text{g}}}+{{F}_{\text{e}}} \right){{r}_{\text{s}}}+2{{F}_{\text{f}}}{{r}_{\text{s}}} $$ (19) $$ \begin{align} & \chi r_{\text{s}}^{\text{3}}\sqrt{\frac{\rho \mu {{\overline{{{u}_{cf}}}}^{3}}}{{{R}^{s}}}}+\frac{\omega \text{ }\!\!\pi\!\!\text{ }\mu _{s}^{2}\overline{{{u}_{\text{cf}}}}}{R}=\frac{4}{3}\text{ }\!\!\pi\!\!\text{ }\Delta ogr_{s}^{3}+{{F}_{\text{e}}}+ \\ & 2\text{ }\!\!\pi\!\!\text{ }m\rho gHr_{\text{s}}^{2} \\ \end{align} $$ (20) 近似的有：
$$ R \approx \sqrt{k / \varphi} $$ (21) $$ \overline{u_{\mathrm{cf}}}=u_{c_{-} i} / \varphi $$ (22) 根据等直径球形颗粒模型，孔隙度的计算为：
$$ \varphi =1-\frac{\text{ }\!\!\pi\!\!\text{ }}{6(1-\cos \theta )\sqrt{1+2\cos \theta }} $$ (23) 将式(21)和(22)代入式(20)：
$$ \begin{align} & \chi r_{\text{s}}^{3}\sqrt{\frac{\rho \mu u_{c-i}^{3}}{{{\varphi }^{3}}\sqrt{\frac{{{k}^{3}}}{{{\varphi }^{3}}}}}}+\frac{\omega \text{ }\!\!\pi\!\!\text{ }\mu r_{s}^{2}{{u}_{c\_i}}}{\varphi \sqrt{\frac{k}{\varphi }}}=\frac{4}{3}\text{ }\!\!\pi\!\!\text{ }\Delta \rho gr_{s}^{3}+{{F}_{\text{c}}}+ \\ & 2\text{ }\!\!\pi\!\!\text{ }m\rho gHr_{s}^{2} \\ \end{align} $$ (24) $ 令\ a=\sqrt{\frac{\mu }{k{{\varphi }^{2}}\sqrt{k/\varphi }}}$
$$ \begin{align} & \chi a\sqrt{\rho }{{(\sqrt{{{u}_{{{c}_{-}}i}}})}^{3}}+\frac{\omega \text{ }\!\!\pi\!\!\text{ }\varphi k{{a}^{2}}}{{{r}_{s}}}{{(\sqrt{{{u}_{{{c}_{-}}i}}})}^{2}}=\frac{4}{3}\text{ }\!\!\pi\!\!\text{ }\Delta og+ \\ & \frac{{{F}_{\text{e}}}}{r_{\text{s}}^{\text{3}}}+\frac{2\text{ }\!\!\pi\!\!\text{ }\mu \rho gH}{{{r}_{s}}} \\ \end{align} $$ (25) 可以解出临界流速uc_i：
$$ \begin{array}{*{35}{l}} \sqrt{{{u}_{c\_i}}}= \\ {{\{{{[{{(-\frac{{{B}^{3}}}{27{{A}^{3}}}+\frac{C}{2A})}^{2}}-\frac{{{B}^{6}}}{729{{A}^{6}}}]}^{0.5}}+\frac{C}{2A}-\frac{{{B}^{3}}}{27{{A}^{3}}}\}}^{\frac{1}{3}}} \\ -\frac{B}{3A}+\frac{{{B}^{2}}}{9{{A}^{2}}{{[{{(\frac{C}{2A}-\frac{{{B}^{3}}}{27{{A}^{3}}})}^{2}}-\frac{{{B}^{6}}}{729{{A}^{6}}}]}^{0.5}}+\frac{C}{2A}-\frac{{{B}^{3}}}{27{{A}^{3}}}} \\ \end{array} $$ (26) $ 其中:A=\chi \sqrt{\rho }\sqrt{\frac{\mu }{k{{\varphi }^{2}}\sqrt{k/\varphi }}}$
$$ \begin{array}{*{35}{l}} B=\frac{\omega \pi \mu }{\varphi \sqrt{\frac{k}{\varphi }}} \\ C=\frac{4}{3}\text{ }\pi \text{ }\Delta \rho g+\frac{{{F}_{e}}}{r_{s}^{3}}+\frac{2\text{ }\pi \text{ }\mu \rho gH}{{{r}_{s}}} \\ \end{array} $$ 3. 敏感性分析
3.1 微粒粒径对临界流速的影响
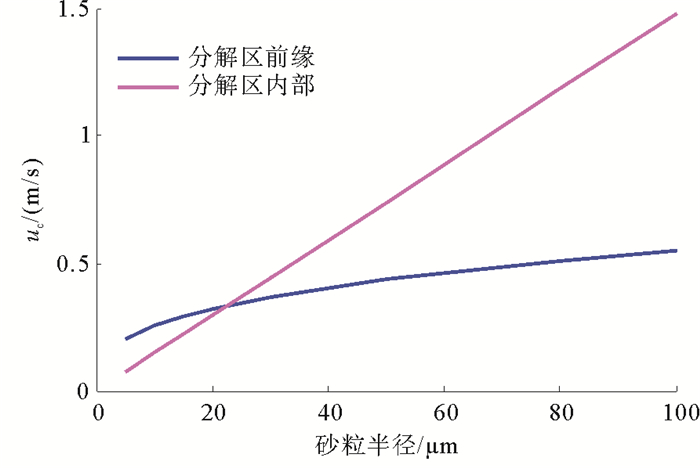
取水的粘度为μ =1.01 mPa·s，地层砂颗粒密度为ρ =2 654 kg/m3，沉积物堆积角度为θ =75°，摩擦系数m =0.3，埋深h =175 m，水深H =500 m。则可以分别根据式(18)和式(26)求出地层砂粒径条件下水合物分解前缘、分解区内部地层砂微粒启动运移流速，如图 3所示。
![]()
图 3 粒径与水合物分解区地层砂微粒启动运移临界流速关系曲线Figure 3. Relationship between diameter and critical velocity of sand migration in hydrate decomposed zone由图 3可知，水合物分解前缘处微粒和分解区内部微粒在液流作用下启动运移的临界流速都随着粒径的增加而增加。当微粒粒径较小时，位于分解区内部的微粒的临界启动运移流速大于位于分解区前缘的微粒，在水合物分解产出过程中，位于水合物分解区前缘处的微粒更容易启动运移，水合物分解产生的空隙沿着液流相反的方向延伸，从而形成类蚯蚓洞结构。当微粒粒径较大时，位于分解区内部的微粒临界启动运移流速小于位于分解区前缘的微粒，在水合物分解产出过程中位于分解区内部的微粒更容易启动运移，使水合物分解产生的孔隙在垂直于液流方向上增大。当液流的流速足够大时，处于水合物分解产生的空隙周围的松散沉积物颗粒都有可能会被携带产出，使整个松散沉积物亏空。
水合物分解区地层砂粒启动运移是一个动态的过程，当流速超过松散沉积物中由于水合物分解产生的空隙周围的微粒的临界启动运移流速时，这些微粒就会启动运移。由于微粒发生启动运移，水合物分解产生的空隙增大，其周围的微粒的临界启动运移流速也相应增大，直到临界启动运移流速小于空隙中的液流流速时，空隙周围微粒的启动运移停止。
基于上述分析，取相同条件下分解区前缘和分解区内部临界启动运移临界流速较小的值作为整个松散沉积物微粒启动运移的临界流速，即：
$$ {{u}_{c}}=\min \left( {{u}_{c\_i}}, {{u}_{c\_f}} \right) $$ (27) 下文将重点分析uc随微粒排布方式、摩擦系数等的变化规律。
3.2 微粒排布规律对临界流速的影响
分别取地层砂微粒半径rs=5、10、15、20、30、50 μm，其他条件同上，则不同沉积物微粒堆积角度下地层砂启动运移的临界流速模拟结果如图 4所示。
![]()
图 4 排布规律和临界启动运移流速关系曲线Figure 4. Relationship between arrangement angle and critical velocity of sand migration in hydrate decomposed zone如图 4所示松散沉积物的微粒临界启动运移流速随着排布角度的增加而增加，当排布角度增加到一定数值时渐渐趋于平稳。这是由于随着排布角度的增加孔隙度增加，空隙内流体的真实渗流流速降低，减小了对微粒的液流拖曳作用，从而导致临界流速增加。
3.3 摩擦系数对临界流速的影响
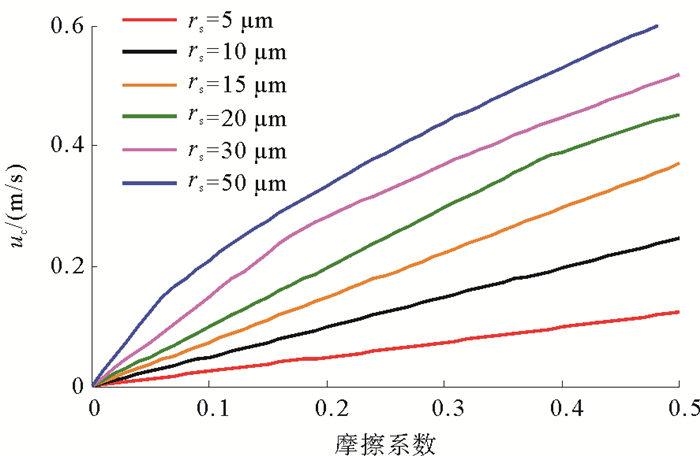
取地层砂微粒半径rs=5、10、15、20、30、50 μm，其他条件同上，得到不同地层砂粒条件下摩擦系数对微粒启动运移临界流速的影响规律分布曲线如图 5所示。
![]()
图 5 摩擦系数与微粒临界启动运移流速关系曲线Figure 5. Relationship between coefficient of friction and critical velocity of sand migration in hydrate decomposed zone由上图可知，微粒临界启动运移流速随摩擦系数增大而增大，这是由于深度恒定的情况下上覆压力恒定，随着摩擦系数的增加摩擦力也增加。而这种情况下摩擦力远大于微粒自身的重力和内聚力，所以摩擦力对水合物分解区前缘地层砂启动运移临界流速影响较大。
3.4 其他影响因素
其他对水合物分解区地层砂启动运移临界流速的影响因素主要有胶结物的性质，流体中的电解质类型、浓度以及上覆岩层压力等。特别地，胶结物的性质主要影响微粒所受到的内聚力的大小，胶结强度越大，内聚力越大，微粒越不容易在液流的拖曳作用下发生移动。流体中的电解质的类型及浓度直接决定了微粒所受到的静电力。电解质浓度越大，微粒的双电层厚度越小，微粒间的静电力也就越大，微粒启动运移临界流速也相应增大。
4. 结论
(1) 天然气水合物开采过程中，天然气水合物分解会导致沉积物松散程度加剧，处于水合物分解前缘和分解区内部的地层砂微粒都有可能在液流的作用下启动运移。粒径较小时，水合物分解区前缘处微粒将优先发生运移；粒径较大时，水合物分解区内部微粒将优先发生运移，地层砂粒启动运移是一个动态过程。
(2) 水合物分解区松散沉积物地层砂微粒启动运移临界流速的大小随着颗粒排布角度、摩擦系数的增大而增大。胶结物的性质，特别是流体中的电解质类型以及浓度等都会对临界出砂流速产生一定的影响。
(3) 根据本文的模拟结果，天然气水合物开采过程中的出砂的起始位置是分解前缘，但随着水合物的分解产出，水合物分解前缘不断推进，地层渗流场也发生实时的变化，因此实际水合物开采过程中的地层出砂现象需要进一步考虑地层渗流场的分布规律，这将是下一步的工作重点。
-
![]()
图 1 天然气水合物松散沉积物中微粒示意图
a.原始条件下地层微粒分布示意图；
b.水合物分解后形成的“孤立悬空”的砂粒示意图；
c.水合物分解前缘砂粒示意图；
d.水合物分解区内部砂粒示意图
蓝色微粒表示天然气水合物，黑色微粒表示地层沉积物骨架，红色微粒表示水合物分解后可能造成的游离颗粒或胶结相对较弱的砂粒Figure 1. Schematic diagram of particles in hydrate decomposed unconsolidated sediment
![]()
图 2 分解区松散沉积物中微粒受力示意图
Figure 2. Force diagram of particles in unconsolidated sediment of hydrate decomposed zone
![]()
图 3 粒径与水合物分解区地层砂微粒启动运移临界流速关系曲线
Figure 3. Relationship between diameter and critical velocity of sand migration in hydrate decomposed zone
![]()
图 4 排布规律和临界启动运移流速关系曲线
Figure 4. Relationship between arrangement angle and critical velocity of sand migration in hydrate decomposed zone
-
[1] Wu N Y, Zhang H Q, Yang S X, et al. Gas hydrate system of Shenhu area, northern South China Sea: geochemical results[J]. Journal of Geological Research, 2011, 2011: Article ID 370298.
[2] Zhang G X, Liang J Q, Lu J A, et al. Geological features, controlling factors and potential prospects of the gas hydrate occurrence in the east part of the Pearl River Mouth Basin, South China Sea[J]. Marine and Petroleum Geology, 2015, 67: 356-367. doi: 10.1016/j.marpetgeo.2015.05.021
[3] 李彦龙, 刘乐乐, 刘昌岭, 等.天然气水合物开采过程中的出砂与防砂问题[J].海洋地质前沿, 2016, 32(7): 36-43. http://d.old.wanfangdata.com.cn/Periodical/hydzdt201607005 LI Yanlong, LIU Lele, LIU Changling, et al. Sanding prediction and sand-control technology in hydrate exploitation: a review and discuss[J]. Marine Geology Frontiers, 2016, 32(7): 36-43. http://d.old.wanfangdata.com.cn/Periodical/hydzdt201607005
[4] Terao Y, Duncan M, Hay B, et al. Deepwater methane hydrate gravel packing completion results and challenges[C]//Offshore Technology Conference. Houston, Texas: Offshore Technology Conference, 2014.
[5] Chong Z R, Yang S H B, Babu P, et al. Review of natural gas hydrates as an energy resource: Prospects and challenges[J]. Applied Energy, 2015, 162: 1633-1652. http://www.sciencedirect.com/science/article/pii/S030626191401318X
[6] Kjorholt H, Joranson H, Markestad P, et al. Advanced sand prediction in a user friendly wrapping[C]//SPE/ISRM Rock Mechanics in Petroleum Engineering. Trondheim, Norway: Society of Petroleum Engineers, 1998.
[7] 董长银, 张清华, 崔明月, 等.复杂条件下疏松砂岩油藏动态出砂预测研究[J].石油钻探技术, 2015, 43(6): 81-86. http://d.old.wanfangdata.com.cn/Periodical/syztjs201506015 DONG Changyin, ZHANG Qinghua, CUI Mingyue, et al. A dynamic sanding prediction model for unconsolidated sandstone reservoirs with complicated production conditions[J]. Petroleum Drilling Techniques, 2015, 43(6): 81-86. http://d.old.wanfangdata.com.cn/Periodical/syztjs201506015
[8] Muller A L, do AmaralVargas Jr E, Vaz L E, et al. Numerical analysis of sand/solids production in boreholes considering fluid-mechanical coupling in a Cosserat continuum[J]. International Journal of Rock Mechanics and Mining Sciences, 2011, 48(8): 1303-1312. doi: 10.1016/j.ijrmms.2011.09.012
[9] Talaghat M R, Esmaeilzadeh F, Mowla D. Sand production control by chemical consolidation[J]. Journal of Petroleum Science and Engineering, 2009, 67(1-2): 34-40. doi: 10.1016/j.petrol.2009.02.005
[10] Papamichos E, Tronvoll J, Skjærstein A, et al. Hole stability of Red Wildmoor sandstone under anisotropic stresses and sand production criterion[J]. Journal of Petroleum Science and Engineering, 2010, 72(1-2): 78-92. doi: 10.1016/j.petrol.2010.03.006
[11] 王静丽, 梁金强, 宗欣, 等.南海北部神狐海域天然气水合物差异性分布的控制因素[J].海洋地质前沿, 2015, 31(1): 24-30. http://d.old.wanfangdata.com.cn/Periodical/hydzdt201501004 WANG Jingli, LIANG Jinqiang, ZONG Xin, et al. Differentiated distribution of methane hydrate in the Shenhu Area of the northern South China Sea and controlling factors[J]. Marine Geology Frontiers, 2015, 31(1): 24-30. http://d.old.wanfangdata.com.cn/Periodical/hydzdt201501004
[12] 李彦龙, 刘昌岭, 刘乐乐.含水合物沉积物损伤统计本构模型及其参数确定方法[J].石油学报, 2016, 37(10): 1273-1279. doi: 10.7623/syxb201610007 LI Yanlong, LIU Changling, LIU Lele. Damage statistic constitutive model of hydrate-bearing sediments and the determination method of parameters[J]. Acta Petrolei Sinica, 2016, 37(10): 1273-1279. doi: 10.7623/syxb201610007
[13] 张光学, 黄永样, 祝有海, 等.南海天然气水合物的成矿远景[J].海洋地质与第四纪地质, 2002, 22(1): 75-81. http://d.old.wanfangdata.com.cn/Periodical/hydzydsjdz200201012 ZHANG Guangxue, HUANG Yongyang, ZHU Youhai, et al. Prospect of gas hydrate resources in the South China Sea[J]. Marine Geology and Quaternary Geology, 2002, 22(1): 75-81. http://d.old.wanfangdata.com.cn/Periodical/hydzydsjdz200201012
[14] Liu C L, Meng Q G, Hu G W, et al. Characterization of hydrate-bearing sediments recovered from the Shenhu area of the South China Sea[J]. Interpretation, 2017, 5(3): 1-39. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=77d2f5c137cf262216acf0faf8f923c0
[15] 张卫东, 王瑞和, 任韶然, 等.天然气水合物储层物理模型[J].石油学报, 2011, 32(5): 866-871. http://d.old.wanfangdata.com.cn/Periodical/syxb201105020 ZHANG Weidong, WANG Ruihe, REN Shaoran, et al. A study on physical models of gas hydrate reservoirs[J]. Acta Petrolei Sinica, 2011, 32(5): 866-871. http://d.old.wanfangdata.com.cn/Periodical/syxb201105020
[16] 董刚, 龚建明, 王家生.从天然气水合物赋存状态和成藏类型探讨天然气水合物的开采方法[J].海洋地质前沿, 2011, 27(6): 59-64. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=hydzdt201106010 DONG Gang, GONG Jianming, WANG Jiasheng. Gas hydrate exploitation methods upon types and occurrence of gas hydrate accumulations[J]. Marine Geology Frontiers, 2011, 27(6): 59-64. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=hydzdt201106010
[17] 吴剑, 常毓文, 穆歌, 等.水驱黏土微粒迁移理论及作用[J].油田化学, 2015, 32(1): 57-61. http://d.old.wanfangdata.com.cn/Periodical/ythx201501013 WU Jian, CHANG Yuwen, MU Ge, et al. Theory and function for clay fines migration in water flooding[J]. Oilfield Chemistry, 2015, 32(1): 57-61. http://d.old.wanfangdata.com.cn/Periodical/ythx201501013
[18] Altmann J, Ripperger S. Particle deposition and layer formation at the crossflow microfiltration[J]. Journal of Membrane Science, 1997, 124(1): 119-128. doi: 10.1016-S0376-7388(96)00235-9/
[19] Gregory J. Approximate expressions for retarded van der Waals interaction[J]. Journal of Colloid and Interface Science, 1981, 83(1): 138-145. doi: 10.1016/0021-9797(81)90018-7
[20] Gregory J. Interaction of unequal double layers at constant charge[J]. Journal of Colloid and Interface Science, 1975, 51(1): 44-51. doi: 10.1016/0021-9797(75)90081-8
[21] Bedrikovetsky P G, Siqueira F D, Furtado C J A, et al. Quantitative theory for fines migration and formation damage[C]//SPE International Symposium and Exhibiton on Formation Damage Control. Lafayette, Louisiana, USA: Society of Petroleum Engineers, 2010.
-
期刊类型引用(14)
1. 吴能友，李彦龙，蒋宇静，孙金声，谢文卫，胡高伟，王韧，于彦江，王金堂，陈强，申凯翔，孙志文，陈明涛. 海洋天然气水合物工程地质学的提出、学科内涵与展望. 地学前缘. 2025(02): 216-229 . 
百度学术
2. 李彦龙，吴能友，王宏斌，纪云开，綦民辉，刘昌岭，万义钊，陈明涛. 海域天然气水合物储层的多场耦合模式及研究进展. 工程地质学报. 2024(04): 1355-1366 . 百度学术
3. 周扬，潘栋彬，曾云霜. 离子型稀土开采过程中导流井井周矿体颗粒脱落运移临界流速研究. 钻探工程. 2024(S1): 112-116 . 百度学术
4. 卢静生，吴思婷，李栋梁，梁德青，魏伟，何勇，史伶俐，邓福成，熊友明. 海洋天然气水合物开采的固相控制策略. 新能源进展. 2022(02): 137-145 . 百度学术
5. 卢静生，林德才，李栋梁，梁德青，张逸群，吴思婷，何勇，史伶俐. 天然气水合物开发的水平井控水控砂完井研究进展. 新能源进展. 2022(05): 447-455 . 百度学术
6. 齐赟，孙友宏，李冰，沈奕锋，张国彪，黄峰. 近井储层改造对天然气水合物藏降压开采特性影响的数值模拟研究. 钻探工程. 2021(04): 85-96 . 百度学术
7. 宁伏龙，方翔宇，李彦龙，窦晓峰，王林杰，刘志超，罗强，孙嘉鑫，赵颖杰，张准，刘天乐，张凌，蒋国盛. 天然气水合物开采储层出砂研究进展与思考. 地质科技通报. 2020(01): 137-148 . 百度学术
8. 李彦龙，刘昌岭，廖华林，董林，卜庆涛，刘志超. 泥质粉砂沉积物—天然气水合物混合体系的力学特性. 天然气工业. 2020(08): 159-168 . 百度学术
9. 宁伏龙，窦晓峰，孙嘉鑫，刘志超，李彦龙，李晓东，赵颖杰，刘昌岭，陆红锋，于彦江，李芷，罗强，曹鑫鑫. 水合物开采储层出砂数值模拟研究进展. 石油科学通报. 2020(02): 182-203 . 百度学术
10. 游利军，邵佳新，王都，王汉，康毅力，陈明君. 储气库碳酸盐岩裂隙微粒运移实验模拟. 特种油气藏. 2020(05): 94-99 . 百度学术
11. 赵景芳，宋林松，吉飞，邓智铭，张剑波，王志远. 天然气水合物降压开采储层出砂数值模拟. 中国海上油气. 2019(02): 116-124 . 百度学术
12. 宋本健，程远方，李庆超，韩忠英，吕亚慧. 水合物分解对海底边坡稳定影响的数值模拟分析. 海洋地质与第四纪地质. 2019(03): 182-192 . 本站查看
13. 卢静生，熊友明，李栋梁，梁德青，金光荣，何勇，申小冬. 非成岩水合物储层降压开采过程中出砂和沉降实验研究. 海洋地质与第四纪地质. 2019(04): 183-195 . 本站查看
14. 董长银，钟奕昕，武延鑫，周玉刚，曾思睿，闫切海. 水合物储层高泥质细粉砂筛管挡砂机制及控砂可行性评价试验. 中国石油大学学报(自然科学版). 2018(06): 79-87 . 百度学术
其他类型引用(17)
下载:
计量
- 文章访问数: 2052
- HTML全文浏览量: 332
- PDF下载量: 19
- 被引次数: 31
